Recursive Fonksiyonlar (Özyineli Fonksiyonlar) Örnekleri ve Konu Anlatımı
C Programlama Dili Recursive fonksiyon örnekleri ve konu anlatımını bulabilirsiniz. Recursive Fonksiyon Avantajları, Dezavantajları ve Bileşenlerinin detayları.
Iteratif fonksiyonlar ve Recursive fonksiyonlar olarak Fonksiyonları ikiye ayırabiliriz. Iteratif fonksiyonlar, do while, while, for gibi döngüler kullanılarak bir işlemi birden fazla kez yapmaya yararlar. Recursive fonksiyonlar da bu döngüler asla kullanılmaz. Eğer bu döngüleri kullanıyorsanız fonksiyonunuza recursive diyemeyiz. Kısaca Recursive Fonksiyon, fonksiyonun kendisini çağırmasıyla bir işlemi birden fazla defa yapmaya yarar.
Recursive Fonksiyon Avantajları
- Bazı durumlarda çok hızlı çalışır.
- Genellikle çok az satır işlemde fonksiyonu yazabilirsiniz. Bu sayede okuması kolay kodlar yazabilirsiniz.
Recursive Fonsiyon Dezavantajları
- Bazı dururumlar sürekli aynı işlemi yapabilir. Bu durumlarda iteratif fonksiyonlara göre yavaş olur.
- Recursive işlemler Stack’de tutulduğundan bellek sorunu ortaya çıkabilir
Recursive Fonksiyon Bileşenleri
- Base Case (Temel durum): Recursive olmayan durum.
- General Case (Genel durum): Recursive durum.
- Convergence (Yakınlaşma): Base Case’e yaklaşma.
Recursive fonksiyon bileşenlerini fibonacci örneği üzerinden anlatmak ve anlamak çok kolay olacaktır.
| F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 |
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 |
Bilindiği üzere fibonacci serisi yukarıdaki gibidir. F3 = F2 + F1 şeklindedir.
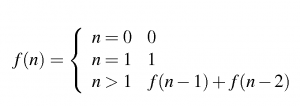
Yukarıdaki şekilde tanımlamasını yapabiliriz.
Fibonacci serisinde sıfırıncı ve birinci değerlerin sonucu bir sayıdır. Yani recursive bir değer değildir. n=0 ve n=1 tanımlamaları Base Case‘di
n>1 durumunda ise f(n-1) + f(n-2) şeklindedir. Yani sonuç yine fonksiyona gitmektedir. Bu durum ise General Case olarak adlandırılmıştır. General Case asıl recursive durumdur.
General Case içerisinde f(n-1) ve f(n-2) görmekteyiz. Girilen n değeri n=0 ve n=1 durumlarına yaklaşmaktadır. Bu durum ise Convergence olarak adlandırılıyor.
Genel tanımlamaları geçtikten sonra faktöriyel örneği üzerinden recursive fonksiyonuna göz atalım.
Iteratif Faktöriyel Fonksiyon Örneği
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
#include <stdio.h> int faktoriyel(int); int main() { int sayi = 6; int sonuc = faktoriyel(sayi); printf("%d! = %d\n", sayi, sonuc); return 0; } int faktoriyel(int x) { int sonuc = 1; for(int i = 1; i<= x; i++) sonuc *= i; return sonuc; } |
Çıktı:
|
1 |
6! = 720 |
Recursive Faktöriyel Fonksiyon Örneği
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
#include <stdio.h> int faktoriyel(int); int main() { int sayi = 4; int sonuc = faktoriyel(sayi); printf("%d! = %d\n", sayi, sonuc); return 0; } int faktoriyel(int x) { if (x <= 1) return 1; return x * faktoriyel(x - 1); } |
Çıktı:
|
1 |
4! = 24 |
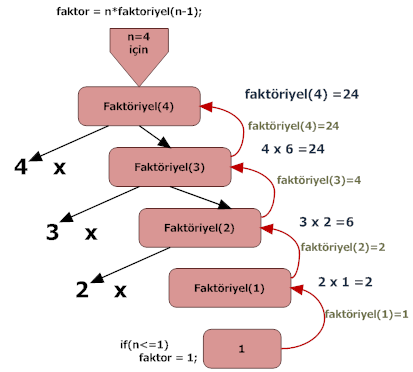
Adım adım recursive fonksiyona bakalım.
- Fonksiyona sayi değişkeni (değeri 4) gönderiliyor.
- 4 <= 1 mi diye kontrol ediliyor ve durumu sağlamadığı için if’i geçiyor.
- return 4* faktoriyel(3) olarak tekrar faktöriyel fonsiyonuna dönüyor. Bu sefer değer 3;
- 3 <= 1 mi diye kontrol ediliyor ve durumu sağlamadığı için if’i geçiyor.
- return 3*faktoriyel(2) olarak tekrar faktöriyel fonsiyonuna dönüyor. Bu sefer değer 2;
- 2<= 1 mi diye kontrol ediliyor ve durumu sağlamadığı için if’i geçiyor.
- return 3*faktoriyel(1) olarak tekrar faktöriyel fonsiyonuna dönüyor. Bu sefer değer 1;
- 1 <= 1 mi diye kontrol ediliyor ve durumu sağlıyor ve 1 değeri geri dönüyor. Bu işlemde sonra adım adım geri gidiyor. Tüm return değerleri stackte tutulmakta ve ilk return değerine gelene kadar stack işlemi devam edecektir.
| faktoriyel(1) = 1 |
| faktoriyel(2) = 2 * faktoriyel(1) |
| faktoriyel(3) = 3 * faktoriyel(2) |
| faktoriyel(4) = 4 * faktoriyel(3) |
Stackteki durum yukardaki tablo da görülmektedir. Faktoriyel 1’in değerini bulduktan sonra stackte bir altındaki işleme geri dönmektedir. Faktöriyel 1’in değeri 1 olduğunu artık biliyoruz.
Faktoriyel 2 ise 2*1 olur ve sonuc 2 olur. Faktöriyel 2’den sonra Faktöriyel 3’e geçiş yapar. Artık faktöriyel 2’nin sonucunu da biliyoruz.
Fakroriyel 3 ise 3*2 olacaktır. Faktöriyel 3’ün ise sonucunu 6 olarak bulduk. Faktöriyel 4 ise 4* faktöriyel 3 olduğundan 4*6’dan 24 olarak sonucu buluruz.
Aşağıdaki tablodan bazı Recursive Fonksiyon örneklerini bulabilirsiniz.